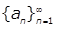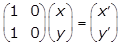Preparation Manual

Domain I—Number Concepts

Competency 001—The teacher understands the real number system and its structure, operations, algorithms and representations.

1. Use the figure below to answer the question that follows.

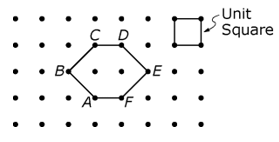
A unit square is drawn in the upper right corner to show that the horizontal or vertical distance between any two adjacent pins is one unit and the area inside is one square unit. In the center of the board is a six-sided figure. The vertices are labeled A, B, C, D, E, and F, with the line between A and F forming the horizontal bottom of the figure. To construct the figure, start at point A, go one unit left and one unit up to point B, one unit right and one unit up to point C, one unit right to point D, one unit right and one unit down to point E, one unit left and one unit down to point F, and one unit left to return to point A.

The figure above represents a geoboard, and each unit square has area 1. Which of the following quantities associated with hexagon ABCDEF is an integer?

1. The length of  BD line B D
2. The area of triangle BCE
3. The area of hexagon ABCDEF
4. The distance from B to the midpoint of  BE line B E

AnswerEnter to expand or collapse answer.Answer expanded

Option C is correct because the area of hexagon ABCDEF is equal to 4 square units, and 4 is an integer. Each unit square has area 1, and the hexagon is composed of 2 full squares and 4 half-squares, for a total area of 2(1) + 4(0.5) = 2 + 2 = 42(1) + 4(0.5) = 2 + 2 = 4. Option A is incorrect because, by the Pythagorean theorem, the length of  BD line BD is √ 2² + 1² the square root of 2 squared plus 1 squared = √ 5 the square root of 5, which is not an integer. Option B is incorrect because the area of triangle BCE is ¹/₂1 half bh = ¹/₂1 half(3)(1) = 1.51 decimal 5, which is not an integer. Option D is incorrect because the distance from B to the midpoint of  BE line B E is ³/₂3 over 2 = 1.51 decimal 5, which is not an integer.

---

2. S is the set of all positive integers that can be written in the form 2ⁿ • 3^m 2 to the power of n times 3 to the power of m, where n and m are positive integers. If a and b are two numbers in S, which of the following must also be in S?

1. a + b
2. √ ab the square root of a times b
3. ^a/_ba over b
4.  ab a times b

AnswerEnter to expand or collapse answer.Answer expanded

Option D is correct because if a and b are two numbers in S, then a = 2^j • 3^ka equals 2 to the power of j times 3 to the power of k and b = 2^s • 3^tb equals 2 to the power of s times 3 to the power of t, where j, k, s, and t are positive integers. So ab = (2^j • 3^k)(2^s • 3^t) = 2^j+s • 3^k+ta b equals left paren 2 to the power of j times three to the power of k right paren left paren 2 to the power of s times 3 to the power of t right paren equals 2 to the power of j plus s times 3 to the power of k plus t, and j + s and k + t are both positive integers; thus ab is in Sj plus s and k plus t are both positive integers; thus a b is in S. Option A is incorrect because, for example, if a = 18 and b = 12, then a + b = 30, which is not in S. Options B and C are incorrect because, for example, if a = 6 and b = 12, then √ ab the square root of a times b = √ 72 the square root of 72 = 6√ 2 the square root of 2 and ^a/_ba over b = ⁶/₁₂6 over 12 = ¹/₂1 half, neither of which is in S.

---

Competency 002—The teacher understands the complex number system and its structure, operations, algorithms and representations.

Use the figure below to answer the question that follows.

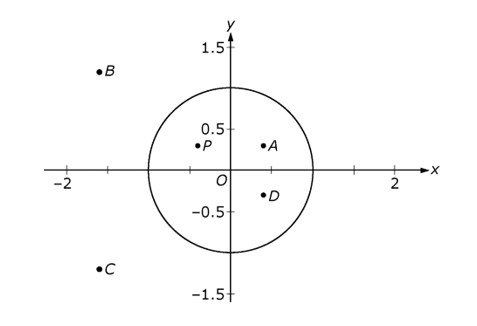
The figure shows a unit circle inscribed around the origin on an x,y coordinate plane. The x axis is marked with values at negative 2 and 2, with tick marks in increments of 0.5. The y axis is marked with values at negative 1.5, negative 0.5, 0.5, and 1.5, with tick marks in increments of 0.5. There is a point labeled P at coordinates negative 0.4, 0.3. There are four additional points, labeled A, B, C, and D. Point A is located at coordinates 0.4, 0.3. Point D is located at coordinates 0.4, negative 0.3. Point B is located at coordinates negative 1.6, 1.2. Point C is located at coordinates negative 1.6, negative 1.2.

3. The figure above shows a unit circle in the complex plane. Which of the following points could represent the multiplicative inverse of the complex number represented by point P, which has coordinates (–0.4negative 0 decimal 4, 0.30 decimal 3)?

1. A
2. B
3. C
4. D

AnswerEnter to expand or collapse answer.Answer expanded

Option C is correct because the multiplicative inverse of a complex number a +  bi b times i is ^a/_{a² + b²}a over a squared plus b squared − ^b/_{a² + b²}b over a squared plus b squared i. Point P represents the complex number –0.4negative 0 decimal 4 + 0.3i0 decimal 3 times i, which has multiplicative inverse ^{–0.4negative 0 decimal 4}/_{(–0.4negative 0 decimal 4)² + (0.30 decimal 3)²}negative 0 decimal 4 over negative 0 decimal 4 squared plus 0 decimal 3 squared − ^{0.30 decimal 3}/_{(–0.4negative 0 decimal 4)² + (0.30 decimal 3)²} i0 decimal 3 over negative 0 decimal 4 squared plus 0 decimal 3 squared times i, or –1.6 negative 1 decimal 6 − 1.21 decimal 2i. This number is represented by the point with coordinates (–1.6negative 1 decimal 6,–1.2negative 1 decimal 2), which can only be point C. Options A and D are incorrect because the multiplicative inverse cannot be obtained by reflecting P across the y-axis and the origin, respectively. Option B is incorrect because the inverse does not lie on the ray OP.

---

Competency 003—The teacher understands number theory concepts and principles and uses numbers to model and solve problems in a variety of situations.

4. Olivia traveled 25 miles in 30 minutes, and then she traveled for an additional 20 minutes. If her average speed for the entire trip was 36 miles per hour (mph), what was her average speed for the final 20 minutes of the trip?

1. 15 mph
2. 20 mph
3. 25 mph
4. 30 mph

AnswerEnter to expand or collapse answer.Answer expanded

Option A is correct. Olivia traveled at an average speed of 36 mph for 50 minutes, or ⁵/₆5 sixths of an hour. This gives a total distance of 36(⁵/₆5 over 6)36 times 5 over 6 = 30 miles. She traveled 25 miles in the first 30 minutes, leaving only 5 miles in the last 20 minutes. A rate of 5 miles in 20 minutes is equivalent to a rate of 15 miles in an hour. Option B is incorrect because if Olivia had traveled at a rate of 20 mph for the last 20 minutes, her average speed for the entire trip would have been ^{25 + 20/₃20 over 3}/_⁵/65 over 625 plus 20 over 3 over 5 over 6 = 38 mph. Option C is incorrect because if Olivia had traveled at a rate of 25 mph for the last 20 minutes, her average speed for the entire trip would have been ^{25 + 25/₃25 over 3}/_⁵/65 over 625 plus 25 over 3 over 5 over 6 = 40 mph. Option D is incorrect because if Olivia had traveled at a rate of 30 mph for the last 20 minutes, her average speed for the entire trip would have been ^{25 + 30/₃30 over 3}/_⁵/65 over 625 plus 30 over 3 over 5 over 6 = 42 mph.

---

5. A researcher measured the length of an object to be k centimeters, where k <is less than 0.000010 decimal 0 0 0 0 1. The researcher expressed the value of k in the form a × 10^ba times 10 to the power of b, where a is a real number and b is an integer. Which of the following could be true about a and b in this situation?

1. –negative 1 ≤is less than or equal to a <is less than 0 and b <is less than –negative 1
2. 1 ≤is less than or equal to a <is less than 10 and b <is less than –negative 1
3. 1 ≤is less than or equal to a <is less than 10 and b >is greater than 1
4. ¹/₂1 half ≤is less than or equal to a <is less than 1 and b >is greater than 1

AnswerEnter to expand or collapse answer.Answer expanded

Option B is correct because 0.00001 = 10^–5 = 10 × 10^–60 decimal 00001 equals 10 to the power of negative 5 equals 10 times 10 to the power of negative 6, k can be of the form a × 10^ba times 10 to the power of b for 1 ≤ a < 101 is less than or equal to a is less than 10 and b < –1b is less than negative 1. For example, if k = 0.000002,0 decimal 000002 then a = 2 and b = –6b equals negative 6. Option A is incorrect because if a is negative, then the value of a × 10^ba times 10 to the power of b will also be negative and thus cannot represent a distance. Option C is incorrect because if 1 ≤ a < 101 is less than or equal to a is less than 10 and b > 1is greater than 1, then a × 10^b > 10a times 10 to the power of b is greater than 10. Option D is incorrect because if ¹/₂1 half ≤is less than or equal to a <is less than 1 and b >is greater than 1, then a × 10^b > 5a times 10 to the power of b is greater than 5.

---

Domain II—Patterns and Algebra

Competency 004—The teacher uses patterns to model and solve problems and formulate conjectures.

6. If left brace a sub n right brace sup infinity sub n equals 1 is a sequence such that a₁ = 1, a₂ = 3, and a_n+3 = ^a_n+1/_an+2a sub 1 equals 1, a sub 2 equals 3, and a sub n plus 3 equals fraction a sub n plus 1 all over a sub n plus 2 for all integers n ≥is greater than or equal to 0, what is the value of a₄a sub 4?

1. 9
2. 7
3. 1
4. ¹/₃1 third

AnswerEnter to expand or collapse answer.Answer expanded

Option A is correct because by the given formula, a₃ = ^a₁/_a2 = ¹/₃ and a₄ = ^a₂/_a3 = ³/_(¹/3) = 9a sub 3 equals a sub 1 over a sub 2 equals 1 third and a sub 4 equals a sub 2 over a sub 3 equals 3 over left paren 1 third right paren equals 9. Option B is incorrect because 7 is the result obtained by adding the two previous terms each time, instead of taking the quotient. Option C is incorrect because 1 is the result obtained by using a_n+3 = ^a_n+2/_an+1a sub n plus 3 equals a sub n + 2 all over a sub n plus 1. Option D is incorrect because ¹/₃1 third is the value of a₃a sub 3 instead of a₄a sub 4.

---

7. A certain finite sequence of consecutive integers begins with –13negative 13. If the sum of all the terms of the sequence is 45, how many terms are there in the sequence?

1. 27
2. 28
3. 29
4. 30

AnswerEnter to expand or collapse answer.Answer expanded

Option D is correct because the terms of the sequence described are the consecutive integers starting at –negative 13, the first 27 terms of the sequence, from –negative 13 to 13, have a sum of 0. The next 3 terms, 14, 15 and 16, have a sum of 45, which is the given sum. So, there are 30 terms in the sequence. Option A is incorrect because the first 27 terms in the sequence have a sum of 0. Option B is incorrect because the first 28 terms in the sequence have a sum of 14. Option C is incorrect because the first 29 terms in the sequence have a sum of 29.

---

Competency 005—The teacher understands attributes of functions, relations and their graphs.

8. Use the graph below to answer the question that follows.

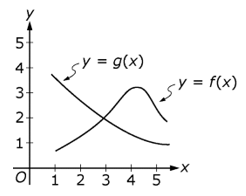
The graph shows two curves on an x, y plane. Both axes are marked with values from 0 to 5 in increments of 1. In the following descriptions, the values are approximate. A curve labeled y = g of x starts at 1, 3.8 and curves smoothly down through 5, 1, starting at about a 45° angle and ending almost horizontally. A curve labeled y = f of x starts at 1, 0.5, curves up at about a 45° angle, becomes slightly steeper around 4, 3, rounds smoothly through a peak value around 4.25, 3.25, then curves smoothly down through 5, 2.

The graphs of the functions f and g are shown in the xy-plane above. For which of the following values of x is the value of g(x)g of x closest to the value of f(2)f of 2?

1. 1
2. 2
3. 3
4. 4

AnswerEnter to expand or collapse answer.Answer expanded

Option D is correct. The value of f(2)f of 2 is a little greater than 1, and so is the value of g(4)g of 4. For the other options, the value of g(x)g of x is not as close to the value of f(2)f of 2 as is the value of g(4)g of 4. Option A is incorrect because g(1)g of 1 is greater than 3. Option B is incorrect because g(2)g of 2 is greater than 2. Option C is incorrect because g(3)g of 3 is about 2.

---

9. Let f be the function defined by f(x)f of x = –negative x + ¹/_x1 over x for all x ≠ 0. Which of the following must be true?

1. f(–negative x)f of negative x = –negative f(x)f of x
2. f(–negative x)f of negative x = f(x)f of x
3. f(¹/_x) = f(x)f of one over x equals f of x
4. f(¹/_x) = – ¹/_f(x)f of one over x equals negative one of f of x

AnswerEnter to expand or collapse answer.Answer expanded

Option A is correct because if f(x)f of x = –negative x + ¹/_x1 over x, then f(–negative x)f of negative x = –negative (–negative x) + ¹/_{–negative x}1 over negative x = x −minus ¹/_x1 over x and –negative f(x)negative f of x = –negative (–negative x + ¹/_x1 over x) = x −minus ¹/_x1 over x. These two functions are equivalent. Option B is incorrect because f(–negative x)f of negative x = –negative (–negative x) + ¹/_{–negative x}1 over negative x = x −minus ¹/_x1 over x is not equivalent to f(x)f of x. Option C is incorrect because f(¹/_x1 over x)f of 1 over x = –negative (¹/_x1 over x) + ¹/_{(¹/x1 over x)}1 over 1 over x = –negative  ¹/_x1 over x + x is not equivalent to f(x)f of x. Option D is incorrect because f(¹/_x1 over x)f of 1 over x = –negative (¹/_x1 over x) + ¹/_{(¹/x1 over x)}1 over 1 over x = –negative  ¹/_x1 over x + x is not equivalent to –negative  ¹/_{f(x)f of x}1 over f of x = –negative   ¹/_{–negative x + ¹/x1 over x}1 over negative x plus 1 over x = –negative  ¹/_{^{–negative x2}/xnegative x-squared over x + ¹/x1 over x}1 over negative x-squared over x plus 1 over x = ^{–negative x}/_{–negative x² + 1}negative x over negative x-squared plus 1 = ^x/_{x² −minus 1}x over x-squared minus 1.

---

Competency 006—The teacher understands linear and quadratic functions, analyzes their algebraic and graphical properties and uses them to model and solve problems.

10. Use the graph below to answer the question that follows.

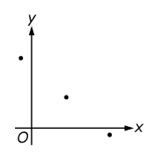
The graph shows three points on an x, y plane. One point is to the left of the y axis and well above the x axis. One point is below the x axis and well to the right of the y axis. One point is about the same distance above the x axis and to the right of the y axis and appears to be halfway between the other two points.

A nonvertical line in the xy-plane can be represented by an equation of the form y = mx + b, where m and b are constants. If line ℓl contains the three points shown, which of the following statements about m and b is true for line ℓl ?

1. m >is greater than 0 and b >is greater than 0
2. m >is greater than 0 and b <is less than 0
3. m <is less than 0 and b >is greater than 0
4. m <is less than 0 and b <is less than 0

AnswerEnter to expand or collapse answer.Answer expanded

Option C is correct because when a line is represented as an equation in the form y = mx + b, m represents the slope and b represents the y-intercept. The line containing the three points shown has a negative slope and a positive y-intercept, so m <is less than 0 and b >is greater than 0. Option A is incorrect because if m >is greater than 0 and b >is greater than 0, the line would have a positive slope. Option B is incorrect because if m >is greater than 0 and b <is less than 0, the line would have a positive slope and a negative y-intercept. Option D is incorrect because if m <is less than 0 and b <is less than 0, the line would have a negative y-intercept.

---

11. Let f be the function defined for all real numbers x by f(x) = (x − a)² + bf of x equals left paren x minus a right paren squared plus b, where a and b are constants such that 0 <is less than a <is less than b. The function f is one-to-one on which of the following intervals?

1. 0 <is less than x <is less than b
2. 0 <is less than x <is less than 2a
3. –negative b <is less than x <is less than b
4. –negative b <is less than x <is less than a

AnswerEnter to expand or collapse answer.Answer expanded

Option D is correct. For a function to be one-to-one on an interval there must be exactly one x-value for each y-value. The graph of the function given is a parabola with vertex at (a, b), where 0 < a < b0 is less than a is less than b. On the interval –b < x < anegative b is less than x is less than a , the parabola consists of points on the left side of the axis of symmetry. For these points, there is exactly one x-value for each y-value, so the function is one-to-one on this interval. Options A, B, and C are incorrect because the portion of the parabola on each of these intervals includes points on both sides of the axis of symmetry. This means that on each interval there are at least 2 points on the parabola with the same y-value but with different x-values.

---

Competency 007—The teacher understands polynomial, rational, radical, absolute value and piecewise functions, analyzes their algebraic and graphical properties and uses them to model and solve problems.

12. Use the graph below to answer the question that follows.

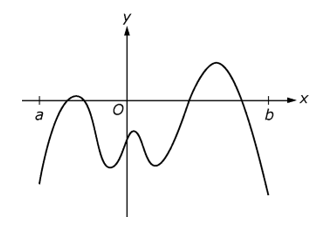
There is a value marked A on the x axis to the left of the y axis. There is a value marked B on the x axis to the right of the y axis. Value B is not quite twice as far from the y axis as value A is. The curve goes up and down several times, turning through smooth curves at each change of direction. The curve starts well below the x axis at value A. It curves up through the x axis then turns a short distance above the x axis to go down almost to its starting y value still to the left of the y axis. It curves up through the y axis and about halfway to the x axis, then turns down again to about the previous y value. It curves back up, passes through the x axis, continues further up than the first peak, then curves back down through the x axis to end somewhat below the original y value at an x value of b.

The xy-plane above shows the graph of y = f(x)y equals f of x on the closed interval [a,b], where f is a polynomial with real coefficients. The function f is strictly increasing for all x < ax is less than a and is strictly decreasing for all x > bx is greater than b. Which of the following statements about f is true?

1. f has 6 real zeros and degree at least 6.
2. f has 4 real zeros and degree at least 6.
3. f has 4 real zeros and degree at most 5.
4. f has 4 real zeros and degree at most 4.

AnswerEnter to expand or collapse answer.Answer expanded

Option B is correct because the fact that the graph intersects the x-axis in four places indicates that the function has 4 real zeros, and the fact that the graph has 5 local extrema indicates that the function has degree at least 6. Option A is incorrect because the graph cannot intersect the x-axis at more than the four places shown given the conditions on f for x <is less than a and x >is greater than b. Options C and D are incorrect because the function must have degree at least 6.

---

13. Use the equation below to answer the question that follows.

Which of the following is an equation of one of the asymptotes of the graph, in the xy-plane, of the equation above?

1. x = –negative 3
2. x = 1
3. y = x −minus 2
4. y = x + 3

AnswerEnter to expand or collapse answer.Answer expanded

Option D is correct because as x approaches ∞infinity or –negative ∞infinity, the value of ¹/_{x − 2}1 over x minus 2 approaches 0; therefore, the value of y = x + 3 + ¹/_{x − 2}y equals x plus 3 plus fraction 1 over x minus 2 approaches y = x + 3. Options A and B are incorrect because the only vertical asymptote of the graph occurs at x = 2. Option C is incorrect because y = x −minus 2 is not an asymptote of the graph.

---

Competency 008—The teacher understands exponential and logarithmic functions, analyses their algebraic and graphical properties and uses them to model and solve problems.

14. Use the figure below to answer the question that follows.

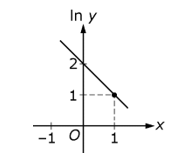
The graph shows a line on an x, y plane. The y axis is labeled l n y and has values marked from 0 to 2 in increments of 1. The x axis has values marked from negative 1 to 1 in increments of 1. The line passes through a value of 2 on the y axis and a point with coordinates 1, 1.

If x and y are related by the line shown above, which of the following equations gives y in terms of x?

1. y = e^x + 2y = e to the power of x + 2
2. y = 2e^xy = 2 e to the power of x
3. y = e^x+2y = e to the power of the quantity x + 2
4. y = e^2−xy = e to the power of the quantity 2 minus x

AnswerEnter to expand or collapse answer.Answer expanded

Option D is correct. Based on the relationship shown in the graph, lny = 2 − x, so y = e^2−xnatural logarithm y equals 2 minus x so y equals e to the power of the quantity 2 minus x. Option A is incorrect because if y = e^x + 2y equals e to the power of x plus 2, then the relationship between lnynatural logarithm y and x would be lny = ln(e^x + 2)natural logarithm y equals natural logarithm left paren e to the power of x plus 2 right paren, which is not represented on the graph. Option B is incorrect because if y = 2e^xy equals 2 e to the power of x, then the relationship between lnynatural logarithm y and x would be lny = ln(2e^x)natural logarithm y equals natural logarithm left paren 2 e to the power of x right paren, which is not represented on the graph. Option C is incorrect because if y = e^x+2y equals e to the power of the quantity x plus 2, then the relationship between lnynatural logarithm y and x would be lny = x + 2natural logarithm y equals x plus 2, which is not represented on the graph.

---

Use the formula and information below to answer the question that follows.

15. Felicia opens a bank account that pays interest compounded continuously at the annual rate of 2.5%. Her initial deposit is $2000, and there will be no other transactions until the amount in her account is $2500. Based on the formula given above, how many years, to the nearest whole number of years, will it take until she has $25002500 dollars in the account?

1. 9
2. 10
3. 11
4. 12

AnswerEnter to expand or collapse answer.Answer expanded

Option A is correct. Based on the formula and information given, 2500 = 2000e^0.025t2500 equals 2000 e to the power of 0.025 t. Solving for t yields t = ^ln1.25/_0.025t equals natural logarithm 1 point 25 all over 0 point 025 ≈approximately equeals 8.98 point 9, which to the nearest whole number is 9. Options B, C, and D are incorrect because they are greater than the number of years it takes for the value of the account to reach $25002500 dollars.

---

Competency 009—The teacher understands trigonometric and circular functions, analyzes their algebraic and graphical properties and uses them to model and solve problems.

Use the figure below to answer the question that follows.

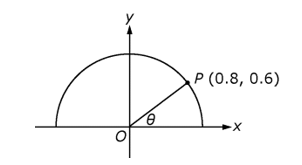
The figure shows a semicircle plotted around the origin on an x, y plane. The semicircle lies entirely above the x axis. Point P lies on the semicircle at coordinates 0.8, 0.6. The angle between the x axis and the radial line ending at point P is labeled theta.

16. In the xy-plane above, point P lies on the semicircle with center O. What is the value of θtheta?

1. coscosine^{–negative 1} 0.60 point 6
2. sinsine^{–negative 1} 0.750 point 7 5
3. sinsine^{–negative 1} 0.80 point 8
4. tantangent^{–negative 1} 0.750 point 7 5

AnswerEnter to expand or collapse answer.Answer expanded

Option D is correct because when a vertical segment is drawn from point P to the x-axis, a right triangle is formed such that the vertical leg has length 0.60 point 6 and the horizontal leg has length 0.80 point 8. Thus, tantangentθtheta = ^0.6/_0.80 point 6 over 0 point 8 = 0.750 point 7 5, and θtheta = tantangent^{–negative 1} 0.750 point 7 5. Option A is incorrect because in the right triangle described above, the length of the hypotenuse is √ 0.6² + 0.8² the square root of 0 point 6 squared plus 0 point 8 squared = 1, so coscosineθtheta = ^0.8/₁0 point 8 over 1 = 0.80 point 8 and θtheta = coscosine^{–negative 1} 0.80 point 8. Options B and C are incorrect because in the right triangle described, sinsineθtheta = ^0.6/₁0 point 6 over 1 = 0.60 point 6 and θtheta = sinsine^{–negative 1} 0.60 point 6.

---

17. Use the figure below to answer the question that follows.

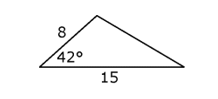
The figure shows a scalene triangle. The horizontal base is dimensioned as 15. The left angle is dimensioned as 42 degrees. The left side is dimensioned as 8.

What is the area of the triangle above?

1. 60 sinsine 42°degrees
2. 60 coscosine 42°degrees
3. 120 sinsine 42°degrees
4. 120 tantangent 42°degrees

AnswerEnter to expand or collapse answer.Answer expanded

Option A is correct because one formula for the area of a triangle is A = ¹/₂1 halfab sinsine C. (Note that b and a sinsine C are the lengths of the base and corresponding altitude.) Applying this formula to the given figure yields A = ¹/₂(8)(15) sin 42° = 60 sin 42°A equals 1 half left paren 8 right paren left paren 15 right paren sine 42 degrees equals 60 sine 42 degrees. Option B is incorrect because cosine is used instead of sine. Option C is incorrect because the ¹/₂1 half in the formula was not used. Option D is incorrect because the ¹/₂1 half in the formula was not used and tangent was used instead of sine.

---

Competency 010—The teacher understands and solves problems using differential and integral calculus.

18. Use the graph below to answer the question that follows.

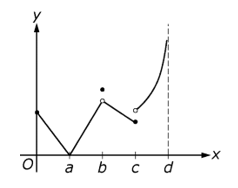
The graph is a plot on an x, y plane. The x axis has equidistant values marked to the right of the origin. They are labeled A, B, C, and D. The first data segment is a straight line from solid point at a value greater than A on the y axis to a solid point at A on the x axis. The second segment is a straight line from point A to a hollow point at a value greater than A directly above point B on the x axis. A short distance above the hollow point is a solid point. The third segment is a straight line from the hollow point to a solid point at a value of A directly above point C on the x axis. A short distance above this solid point is a hollow point. From this hollow point, the fourth data segment rises in a curve of increasing slope that extends off the top of the graph as it approaches value D on the x axis.

The graph of the function f on the interval 0 ≤ x < d 0 is less than or equal to x is less than d is shown above, where 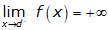. For which of the following values of x does f have a removable discontinuity?

1. a
2. b
3. c
4. d

AnswerEnter to expand or collapse answer.Answer expanded

Option B is correct because at x = b the limit of the function exists but does not equal the value of the function. Option A is incorrect because the function is continuous at x = a. Option C is incorrect because the limit of the function does not exist at x = c. Option D is incorrect because the function has a vertical asymptote at x = d.

---

Domain III—Geometry and Measurement

Competency 011—The teacher understands measurement as a process.

Use the information below to answer the question that follows.

19. A certain roof consists of 2 rectangular sides, each having dimensions 15 feet by 60 feet. Based on the information above, if shingles cost $28.9928 dollars, 99 cents per bundle, which of the following represents the total cost of the shingles for the roof?

1. ^{(3)(2)(15)(60)($28.9928 dollars, 99 cents)}/₁₀₀3 times 2 times 15 times 60 times 28 dollars, 99 cents all over 100
2. ^{(2)(15)(60)($28.9928 dollars, 99 cents)(100)}/₃2 times 15 times 60 times 28 dollars, 99 cents times 100 all over 3
3. ^{(2)(15)(60)($28.9928 dollars, 99 cents)}/_(3)(100)2 times 15 times 60 times 28 dollars, 99 cents all over 3 times 100
4. ^{(3)($28.9928 dollars, 99 cents)(100)}/_(2)(15)(60)3 times 28 dollars, 99 cents times 100 all over 2 times 15 times 60

AnswerEnter to expand or collapse answer.Answer expanded

Option A is correct because the total area of the roof is (2)(15)(60)2 times 15 times 60ft²feet squared. The total cost of the shingles for the roof can be found with the following unit analysis: (2)(15)(60)2 times 15 times 60ft²feet squared ×times ^{1 square of shingles}/_{100ft²feet squared}1 square of shingles over 100 feet squared ×times ^{3 bundles}/_{1 square of shingles}3 bundles over 1 square of shingles ×times ^{$28.9928 dollars, 99 cents}/_{1 bundle}28 dollars, 99 cents over 1 bundle. So by canceling the units, the total cost is ^{(2)(15)(60)(3)($28.9928 dollars, 99 cents)}/₁₀₀2 times 15 times 60 times 3 times 28 dollars, 99 cents all over 100, which is equivalent to option A. Options B, C and D are incorrect because they are not equivalent to ^{(2)(15)(60)(3)($28.9928 dollars, 99 cents)}/₁₀₀2 times 15 times 60 times 3 times 28 dollars, 99 cents all over 100.

---

20. Use the figure below to answer the question that follows.

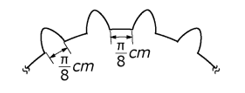
The figure shows a portion of a gear that has cogs evenly spaced around the circumference of a wheel. Each cog is pi over 8 centimeters wide, and there is a space of pi over 8 centimeters between consecutive cogs.

The figure shows a portion of a gear that has cogs evenly spaced around the circumference of a wheel. Each cog is ^πpi/₈pi over 8 centimeters wide, and there is a space of ^πpi/₈pi over 8 centimeters between consecutive cogs. If the diameter of the wheel is 9 centimeters, how many cogs are on the wheel?

1. 12
2. 18
3. 24
4. 36

AnswerEnter to expand or collapse answer.Answer expanded

Option D is correct because the circumference of the wheel is 9π9 pi cm and each cog and space requires a total length of ^πpi/₄pi over 4 cm. The number of cogs that will fit around the wheel with spaces in between is ^{9π9 pi}/_{(^πpi/4pi over 4)}9 times pi over pi over 4 = 36 cogs. Option A is incorrect because 12 cogs and spaces would require a circumference of only 3π3 pi cm. Option B is incorrect because 18 cogs and spaces would require a circumference of only 4.5π4 point 5 pi cm. Option C is incorrect because 24 cogs and spaces would require a circumference of only 6π6 pi cm.

---

Competency 012—The teacher understands geometries, in particular Euclidian geometry, as axiomatic systems.

Use the figure below to answer the question that follows.

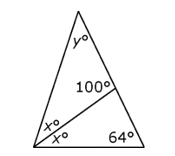
The figure shows a triangle with a horizontal base that is shorter than its two sides. The angle at the right end of the base is dimensioned as 64°. The angle at the top is dimensioned as y°. The angle at the left end of the base is bisected by a line that intersects the opposite side. Each resulting angle at the left end of the base is dimensioned as x°. Where the bisecting line intersects the opposite side, the upper angle is dimensioned as 100°.

21. What is the value of y in the triangle above?

1. 36
2. 40
3. 44
4. 48

AnswerEnter to expand or collapse answer.Answer expanded

Option C is correct. Based on the lower triangle, x + 64 = 100, so x = 36. Then, based on the upper triangle, y + 36 + 100 = 180, so y = 44. Option A is incorrect because 36 is the value of x, not y. Option B is incorrect because if y = 40, then x = 40. Option D is incorrect because if y = 48, then x = 32.

---

Competency 013—The teacher understands the results, uses and applications of Euclidian geometry.

Use the figure below to answer the question that follows.

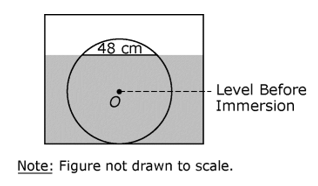
The figure shows a circle that represents a wheel inscribed inside a rectangle that represents a vat of fluid. The wheel sits on the bottom of the vat, and the fluid comes nearly to the top of the wheel. A cord is drawn near the top of the wheel at the level of the fluid. The cord is dimensioned as 48 cm. The origin is labeled Level Before Immersion. There is a note that says Figure not drawn to scale.

22. A wheel with center O and radius 25 cm is immersed in a vat of cleaning solution, as shown in the figure above. The chord of length 48 cm indicates the solution level after the wheel was immersed. The dashed line indicates the solution level before the wheel was immersed. What is the level of the solution in the vat after the wheel has been immersed?

1. 32 cm
2. 33 cm
3. 35 cm
4. 37 cm

AnswerEnter to expand or collapse answer.Answer expanded

Option A is correct. The level of the solution before immersion is the same as the height of the center of the wheel, which is equal to the radius of the wheel, 25 cm. The height of the solution above the center of the wheel can be found by connecting the center of the wheel to the midpoint and to one endpoint of the chord, forming a right triangle with hypotenuse of length 25 cm and one leg of length 24 cm. The length of the third leg can be found to be 7 cm by the Pythagorean theorem and is equal to the height of the solution above the center of the wheel. So the total height of the water after immersion is 25 + 7 = 32 cm. Options B, C, and D are incorrect because the level of the solution after immersion has been shown to be 32 cm.

---

Use the figure below to answer the question that follows.

Line B D is horizontal. Line A B, dimensioned as 8, is vertical, forming a right angle at point B. Line D E is vertical, forming a right angle at point D. Point C lies on line B D. Lines A C and C E form a right angle with each other. Line A C is dimensioned as 10.

23. In the figure above, C is a point on  BD line BD. Triangles ABC and CDE are right triangles, and  AC ⊥ CE line A C is perpendicular to line C E. If the length of  BD line BD is 30, what is the length of  DE line D E?

1. 18
2. 20
3. 24
4. 32

AnswerEnter to expand or collapse answer.Answer expanded

Option A is correct. Angle ACB must be complementary to both ∠DCEangle D C E and ∠BACangle B A C, so ∠BAC ≅ ∠DCEangle B A C is congruent to angle D C E, and △ABCtriangle A B C is similar to △CDEtriangle C D E by the AA similarity criterion. Because the triangles are similar, ^AB/_BC = ^CD/_DEA B over B C equals C D over D E. By applying the Pythagorean theorem to △ABCtriangle A B C, BC = 6. Then CD = 24, because BD = 30 and BC = 6. Substituting the known lengths into the proportion yields ⁸/₆ = ²⁴/_DE8 over 6 equals 24 over D E, which can be solved to show DE = 18D E equals 18. Option B is incorrect because doubling the length of segment  AC line A C does not equal 18. Option C is incorrect because 24 is the length of segment  CD line CD, not the length of segment  DE line D E. Option D is incorrect because 32 = AB + CD32 equals A B + C D, which is much greater than the length of segment  DE line D E.

---

Competency 014—The teacher understands coordinate, transformational and vector geometry and their connections.

Use the matrix equation below to answer the question that follows.

The matrix equation has the following form: a 2 by 2 matrix times a 1 by 1 matrix equals a 1 by 1 matrix. In the first matrix, row 1 is 1, 0, and row 2 is 1, 0. In the second matrix, row 1 is x, and row 2 is y. In the resulting matrix, row 1 is x prime, and row 2 is y prime.

24. The matrix equation above defines a transformation of the xy-plane. Which of the following shows a point P and its image P′P prime under this transformation?

1. Line x = y passes through the origin and point P prime at 1, 1. There is a solid line from point P to point P prime, which continues as a dashed line to the x axis, where it is dimensioned as being perpendicular to the x axis.
2. Point P prime is below the x axis. A line from point P to point P prime is dimensioned as perpendicular to the x axis. The segments from point P to the x axis and from point P prime to the x axis are marked as being congruent.
3. Point P prime lies on the x axis. A line from point P to point P prime is dimensioned as perpendicular to the x axis.
4. Point P prime is to the left of the y axis. A line from point P to point P prime is dimensioned as perpendicular to the y axis. The segments from point P to the y axis and from point P prime to the y axis are marked as being congruent.

AnswerEnter to expand or collapse answer.Answer expanded

Option A is correct because multiplying the left side of the given matrix equation gives 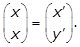. This corresponds to the transformation of a point (x, y) to the point (x, x), as shown in option A. Option B is incorrect because the graph corresponds to the transformation of a point (x, y) to the point (x, –y)(x, negative y). Option C is incorrect because the graph corresponds to the transformation of a point (x, y) to the point (x, 0). Option D is incorrect because the graph corresponds to the transformation of a point (x, y) to the point (–x, y)( negativex, y).

---

Domain IV—Probability and Statistics

Competency 015—The teacher understands how to use appropriate graphical and numerical techniques to explore data, characterize patterns and describe departures from patterns.

Use the definition below to answer the question that follows.

The bulb life, in hours, for 27 lightbulbs of the same brand is recorded below.

275	400	431	465	480	495
350	400	436	465	481	595
360	420	450	470	483
380	425	452	473	490
395	428	460	474	492

275

400

431

465

480

495

350

400

436

465

481

595

360

420

450

470

483

380

425

452

473

490

395

428

460

474

492

25. Based on the definition above, which of the numbers 275 and 595 is an outlier?

1. Neither 275 nor 595
2. 275 only
3. 595 only
4. Both 275 and 595

AnswerEnter to expand or collapse answer.Answer expanded

Option B is correct because the first quartile is 400 and the third quartile is 480, so the interquartile range is 80. By the definition given, any data point that is greater than 1.5(80) = 1201.5 left paren 80 right paren equals 120 above the third quartile or below the first quartile is considered an outlier. So any data point greater than 600 or less than 280 is an outlier. Thus, 275 is an outlier and 595 is not. Option A is incorrect because 275 is an outlier. Options C and D are incorrect because 595 is not an outlier.

---

Competency 016—The teacher understands concepts and applications of probability.

26. A computer company employs over 4000 employees, of whom 45% are women. If a focus group of 20 randomly selected employees is to be formed, what is the expected number of men in the focus group?

1. 8
2. 9
3. 11
4. 13

AnswerEnter to expand or collapse answer.Answer expanded

Option C is correct. If 45% of the employees are women, then 55% of the employees are men. So in a random sample of 20 employees, the expected number of men is 0.55(20) = 11. Options A, B and D are incorrect because it has been shown that the expected number of men must be 11.

---

Competency 017—The teacher understands the relationships among probability theory, sampling and statistical inference and how statistical inference is used in making and evaluating predictions.

Use the graph below to answer the question that follows.

There are two normal curves. The normal curve labeled X has a higher, narrower peak than the normal curve labeled Y.

27. The battery life, in years, for each of two brands of car batteries, X and Y, is approximately normally distributed, as shown above. Which of the following statements about the mean and standard deviation of battery life for the two distributions is true?

1. The mean battery life for X is less than the mean battery life for Y.
2. The mean battery life for X is greater than the mean battery life for Y.
3. The standard deviation of battery life for X is less than the standard deviation of battery life for Y.
4. The standard deviation of battery life for X is greater than the standard deviation of battery life for Y.

AnswerEnter to expand or collapse answer.Answer expanded

Option C is correct because the curve for battery X is steeper and less spread out than the curve for battery Y, indicating that the standard deviation for battery X is less than that for battery Y. Options A and B are incorrect because both curves peak at the same value, indicating the same mean. Option D is incorrect because the standard deviation for battery X is less than that for battery Y.

---

28. To evaluate a new medication that was developed to reduce the occurrence of headaches, a randomized controlled experiment is conducted. One-third of the patients are given the new medication, one-third are given a placebo, and one-third are given nothing. Which of the following is the best example of the placebo effect for this study?

1. People taking the placebo report more headaches than people taking the new medication.
2. People taking the placebo report fewer headaches than people taking the new medication.
3. People taking the placebo report more headaches than people taking nothing.
4. People taking the placebo report fewer headaches than people taking nothing.

AnswerEnter to expand or collapse answer.Answer expanded

Option D is correct because the placebo effect refers to a perceived or actual improvement by the group receiving the placebo compared to the group receiving no treatment. Options A and B are incorrect because each compares the group receiving the placebo to the group receiving the treatment, not to the group receiving no treatment. Option C is incorrect because the placebo effect should show an improvement in the group receiving the placebo.

---

Domain V—Mathematical Processes and Perspectives

Competency 018—The teacher understands mathematical reasoning and problem solving.

Use the statement below to answer the question that follows.

If x²x squared is even, then x is even.

29. A student is trying to prove that the statement above is true for all integers x by proving its contrapositive. Which of the following procedures should the student follow in order to use this method of proof?

1. Assume that x²x squared is even, and then deduce that x is even
2. Assume that x²x squared is not even, and then deduce that x is not even
3. Assume that x²x squared is even, and then deduce that x is not even
4. Assume that x is not even, and then deduce that x²x squared is not even

AnswerEnter to expand or collapse answer.Answer expanded

Option D is correct because the contrapositive of the given statement is "If x is not even, then x²x squared is not even." This statement can be proven by assuming that x is not even and deducing that x²x squared is not even. Option A is incorrect because it describes a method for proving the original statement, but it does not describe the contrapositive. Option B is incorrect because it describes a method for proving the inverse of the original statement. Option C is incorrect because it does not describe the contrapositive.

---

Competency 019—The teacher understands mathematical connections both within and outside of mathematics and how to communicate mathematical ideas and concepts.

Use the problem below to answer the question that follows.

Working together at their constant rates, hoses A and B can fill an empty pool in 10 hours. Working alone, it takes hose B twice as many hours as hose A to fill the pool. How many hours would it take hose A, working alone at its constant rate, to fill the pool?

30. In the problem above, if x represents the number of hours it takes hose A to fill the pool working alone, which of the following equations correctly models the situation?

1. ¹/_x + ¹/_2x = ¹/₁₀1 over x plus 1 over 2x equals 1 over 10
2. ¹/_x + ²/_x = ¹/₁₀1 over x plus 2 over x equals 1 over 10
3. ¹/_x + ¹/_2x = 101 over x plus 1 over 2x equals 10
4. x + 2x = 10x + 2x equals 10

AnswerEnter to expand or collapse answer.Answer expanded

Option A is correct because if hose A can fill the empty pool in x hours, then hose B can fill the empty pool in 2x hours. The fractions of the pool that hoses A and B can each fill in 1 hour are ¹/_x1 over x and ¹/_2x1 over 2x respectively. Working together, it takes the two hoses 10 hours to fill the empty pool, so ¹/₁₀1 tenth of the pool can be filled in 1 hour. Thus, ¹/_x + ¹/_2x = ¹/₁₀1 over x plus 1 over 2x equals 1 over 10. Option B is incorrect because it takes 2x hours for hose B to fill the pool, not ^x/₂x over 2 hours. Option C is incorrect because the combined hourly rate equals ¹/₁₀1 tenth not 10. Option D is incorrect because the total combined time is not equal to the sum of the individual times.

---

Domain VI—Mathematical Learning, Instruction and Assessment

Competency 020—The teacher understands how children learn mathematics and plans, organizes and implements instruction using knowledge of students, subject matter and statewide curriculum (Texas Essential Knowledge and Skills [TEKS]).

31. Of the following activities involving the quadratic expression ax² + bx + cax squared plus bx plus c, which best exemplifies inquiry-based learning?

1. Students predict how the graph of y = ax² + bx + cy equals ax squared plus bx plus c will be affected by changing the value of a, and check their predictions using a graphing calculator.
2. Students solve an equation of the form ax² + bx + c = 0ax squared plus bx plus c equals 0 by graphing the equation on a graphing calculator.
3. Students derive the quadratic formula by completing the square on the left side of the equation ax² + bx + c = 0ax squared plus bx plus c equals 0.
4. Students use a function of the form f(x) = ax² + bx + cf of x equals ax squared plus bx plus c to model a problem involving falling bodies.

AnswerEnter to expand or collapse answer.Answer expanded

Option A is correct because inquiry-based learning refers to the practice of allowing students to explore an idea or question on their own. In the described activity, the students use their calculators to explore the effect on the graph of changing the value of a. Options B, C and D are incorrect because they do not describe an activity in which students explore an idea or question on their own.

---

Competency 021—The teacher understands assessment and uses a variety of formal and informal assessment techniques to monitor and guide mathematics instruction and to evaluate student progress.

32. If a student mistakenly states that – ¹/₂(– ²/₃x + ¹/₂) = ¹/₃x + ¹/₂negative 1 half left paren negative 2 thirds x plus 1 half right paren equals 1 third x plus 1 half, it is most likely that the mistake results from a misunderstanding of which of the following?

1. Multiplication of fractions
2. Arithmetic of negative numbers
3. Associative property of multiplication
4. Distributive property of multiplication over addition

AnswerEnter to expand or collapse answer.Answer expanded

Option D is correct because the student multiplied only the first term in the parenthesis by – ¹/₂negative 1 half, thus making a mistake in the use of the distributive property. Options A and B are incorrect because the student multiplied – ¹/₂negative 1 half by – ²/₃negative 2 thirds correctly. Option C is incorrect because the work does not show an error in the application of the associative property of multiplication.

---